
Die ersten drei Teile der Beitragsreihe zur Vorstellung der Wertungsmethoden, ihrer Vor- und Nachteile und der Frage, für welche Art von Ausschreibung welche Methode geeignet erscheint, haben sich mit den im öffentlichen Auftragswesen bekannten bzw. gängigen Formeln und Verfahrensweisen befasst; Methoden, die im Übrigen auch im cosinex Vergabemanagementsystem zur Verfügung stehen.
Der vierte und letzte Teil befasst sich mit Ansätzen, die im Bereich der Privatwirtschaft durchaus gängige Praxis sind, bislang aber im Umfeld öffentlicher Ausschreibungen wohl noch eher selten angewandt werden: der (einstufigen) Interpolationsmethode sowie der sogenannten Dateneinhüllungsanalyse als Alternative zu der im dritten Teil vorgestellten erweiterten Richtwertmethode, um diejenigen Angebote zu identifizieren, zwischen denen im Rahmen eines zweistufigen Bewertungsverfahrens die Endauswahl erfolgen sollte.

Der Autor
Dr. Stefan Marinus Krusenbaum ist promovierter Wirtschaftswissenschaftler und verantwortet das Controlling der cosinex. Der der Experte für Wertungsmethoden bietet das beliebte Seminar Grundlagen und Auswahl geeigneter Wertungsmethoden in der cosinex Akademie an.
Alle Teile der Reihe
- Teil 1 befasst sich neben einer Einführung mit der Wertungsmethode niedrigster Preis.
- Teil 2 gibt einen Überblick über die Methoden der Wertungsklasse Preis-Kriterien-Gewichtungen.
- Teil 3 analysiert die Wertungsklasse der Richtwert-Methoden.
- Teil 4 stellt weitere, im Bereich des öffentlichen Auftragswesens noch nicht gängige, Wertungsmethoden vor.
Die Interpolationsmethode
Neben den bislang vorgestellten Methoden besteht auch die Möglichkeit, auf die direkte Gegenüberstellung der Preiskriterien und der Leistungskriterien zu verzichten und die Preise stattdessen in Leistungspunktzahlen umzurechnen. Durch diese Vorgehensweise entfällt zwar nicht die Vergabe eines spezifischen Gewichtes, mit dem der Preis als Kriterium (in einen Kriterienbaum) einfließt, jedoch wird hierdurch vermieden, dass es zu Wertungsverzerrungen aufgrund starker Abweichungen bei Preisen und Leistungspunkten kommt. Für die Umrechnung von Preisen in Leistungspunktzahlen bietet sich dem Grunde nach die Anwendung einer sogenannten linearen Interpolation an, wobei von der Anwendung einer solchen Methode in der Regel abzuraten ist, wie im Folgenden näher erläutert wird.
Die Preise müssen bei der linearen Interpolation zur Ermittlung von Preispunkten nicht – wie andere qualitative Leistungskriterien – mithilfe einer Checkliste beurteilt werden, da die Preise der eingegangenen Angebote bereits eine quantitative Basis darstellen und somit in Punktwerte umgerechnet werden können. Um die Preise in Leistungspunkte umzurechnen, wird dabei für gewöhnlich folgende Formel herangezogen:
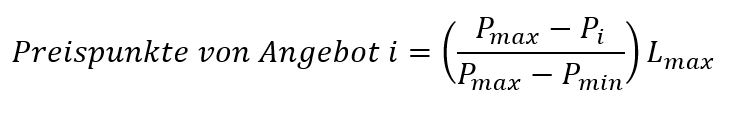
Die Differenz des Preises eines Angebots (i) zum maximalen Preis wird hierbei in Relation zum insgesamt vorliegenden Preisspektrum gesetzt. Das Ergebnis wird mit der maximal erzielbaren Punktzahl L(max) für das Kriterium Preis (z.B. 100 Punkte) multipliziert. Somit wird bezogen auf eine maximal erzielbare Punktzahl eingeordnet, wo sich das gerade betrachtete Angebot auf der Skala zwischen dem höchsten und dem niedrigsten Preis befindet.
Beim Angebot mit dem niedrigsten Preis sind Zähler (P(max) – P(i)) und Nenner (P(max) – P(min)) des Bruchs identisch, somit ergibt sich für den Klammerausdruck der Wert 1 und insgesamt die maximale Punktzahl L(max) als Preispunktzahl. Für das Angebot mit dem höchsten Preis nimmt der Zähler hingegen den Wert 0 an ((P(max) – P(i)) = (P(max) – P(min)) = 0), sodass sich für den Klammerausdruck und damit auch für die Gesamtpunktzahl der Wert 0 ergibt. Alle übrigen Angebote werden durch die Formel je nach ihrem relativen Abstand zum besten Preis linear dazwischen verortet.
Die so ermittelte Preispunktzahl wird anschließend gewichtet und mit der gewichteten Leistungspunktzahl aus den übrigen Entscheidungskriterien verrechnet, um auf die höchste Gesamtpunktzahl zu schließen.
In der Vergabepraxis ist ein solches – an sich schlüssiges – Instrument allerdings insbesondere dann ungeeignet, wenn nur wenige (z.B. zwei) Angebote eingehen, da dann automatisch das schlechtere Angebot (unabhängig davon, wie viel schlechter es ist) den Wert 0 in Bezug auf die Preispunktzahl erhält. Das OLG Düsseldorf geht für diesen Fall (Interpolation bei zwei Angeboten) in seinem Beschluss vom 22.01.2014, VII – Verg 26/13 sogar von einer Rechtswidrigkeit der Methode aus. Indem die vom Angebot mit der niedrigsten Wertungspunktzahl erreichten Wertungspunkte so „unter den Tisch fallen“ würden, missachte der Auftraggeber die Selbstbindung an das von ihm bekannt gegebene Kriterium des wirtschaftlich günstigsten Angebots und die Gewichtung der Unterkriterien, da die Methode im Extremfall auch bei nah zusammenliegenden Preisen die Werte 100 oder 0 für den Angebotspreis ausgibt.
Ein solches Verfahren birgt selbst dann Risiken, wenn sicher davon ausgegangen wird, dass eine ausreichend hohe Anzahl an Angeboten mit überdies hoher Preisvolatilität eingehen wird. Da insbesondere letzteres häufig unbekannt ist, kann die Tauglichkeit dieses Ansatzes in der Regel nicht sichergestellt werden: Das teuerste Angebot erhält immer den Wert 0, unabhängig davon, dass es ggf. nur minimal teurer als andere Angebote ist, was unzulässig ist.
Herausforderungen der bislang vorgestellten Wertungsmethoden
Bei allen bislang vorgestellten Methoden besteht jeweils das Problem, dass der Anwender bestimmte Gewichte, Referenzwerte oder Grenzen selbst explizit angeben muss.
Wird also z.B. im Rahmen einer bloßen Gewichtung von Preis und Leistung (Teil 2 der Beitragsreihe) eine Gewichtung unbegründet nur nach eigenen Präferenzen angegeben, besteht im Zweifel das Risiko, dass eine so getroffene Entscheidung vor einer Vergabekammer nicht standhält; in jedem Fall existiert hierbei aus methodischer Sicht der negative Aspekt, dass die gefundene Lösung mit der selbst gewählten Kriteriengewichtung variiert. Bei Preis-Kriterien-Gewichtungen, bei denen Referenzwerte herangezogen werden, besteht das (zusätzliche) Risiko von Verzerrungen durch einen ungeeigneten Referenzwert.
Die Herausforderung eines Auftraggebers, eine möglichst passende Einbeziehung von Preis- und Leistungskriterien zu erzielen, wird auch durch die Nutzung von Kriterien-Preis-Verhältnissen (Teil 3 der Beitragsreihe) nicht gänzlich gelöst. Zwar ermöglichen diese eine Berücksichtigung beider Kriterien, ohne dass die Vergabestelle selbst eine Gewichtung der Kriterien vornehmen muss, da zur Bildung einer Wertungskennzahl die Leistung hier relativ (d.h. in Bezug auf den mit dieser Leistung einhergehenden Preis) einfließt. Durch diese Vorgehensweise bzw. die implizite Gegenüberstellung von Leistung und Preis als gleichermaßen wichtige Wertungsbestandteile entfällt die Abhängigkeit der Wertungskennzahl von externen Gewichtungsangaben des Anwenders, was den Vorteil dieser Methodik darstellt. Trotzdem kann es auch hier – je nach Datengrundlage – z.B. zur Wahl relativ teurer Angebote kommen, wenn nur die Leistung hinreichend gut ausfällt. Andererseits kann die Wertungskennzahl auch bei einer schlechten Leistungskennzahl hoch ausfallen, wenn nur der Preis ausreichend gering ist.
Nimmt der Anwender, um dieses in einer einfachen (einphasigen) Richtwertmethode auftretende Problem zu verhindern, eine zweiphasige bzw. zweistufige Wertung anhand der erweiterten Richtwertmethode vor, besteht wiederum die Gefahr, dass er durch die Vorgabe, welcher prozentuale Anteil der besten Angebote nochmals gesondert nach dem bestimmten Kriterium betrachtet werden soll, eine zu große oder zu kleine Menge von Angeboten auswählt, zwischen denen erneut nach einem bestimmten Kriterium entschieden wird. Bei allen im dritten Teil dieser Beitragsreihe vorgestellten Richtwertmethoden werden Angebote schon mit einem (leicht) schlechteren Preis-Leistungsverhältnis zudem immer benachteiligt, obwohl es inhaltlich in vielen Fällen auch gut begründbar wäre, dass mit einer höheren Leistung auch ein überproportional höherer Preis einhergehen darf bzw. dass eine niedrigere Leistung eigentlich nur dann akzeptabel ist, wenn damit auch ein unterproportional niedrigerer Preis verbunden ist.
Will man nicht nur subjektive Einflüsse in der Gewichtung ausschließen, sondern auch die Vorgabe von Referenzwerten, muss eine Methode herangezogen werden, die zum einen die Grundprinzipien der Kriterien-Preis-Verhältnisse aufweist (also Leistungen relativ zu ihrem Preis beurteilt), zum anderen muss sie gewährleisten, dass bei einer späteren Auswahl unter einer Gruppe gleichguter Angebote nur solche zur Auswahl stehen, die auch tatsächlich „gleich gut“ sind. Hierbei soll zudem keine weitere Selektion auf Grundlage eigenen Ermessens bzw. selbst gewählter Grenzwerte erfolgen.
Ein Instrument, das dies gewährleistet, ist eine Effizienzanalyse bzw. eine darauf aufbauende Technik zur Messung der relativen Effizienz wie die sogenannte Data Envelopment Analysis (zu deutsch: Dateneinhüllanalyse).
Die Idee der Dateneinhüllanalyse (DEA)
Die Bezeichnung dieses Verfahrens rührt von der grafischen Veranschaulichung verschiedener Alternativen bzw. Angebote, die mit einem Rand umschlossen („eingehüllt“) werden. Im Folgenden wird diese Verfahrensidee in Grundzügen dargestellt.
Die eingegangenen Angebote werden dazu in einem Diagramm einander grafisch gegenübergestellt. Zur besseren Darstellung werden die Preise und Leistungspunktzahlen des Angebots im Folgenden jeweils (normiert) auf Skalen von 1 bis 10 dargestellt.
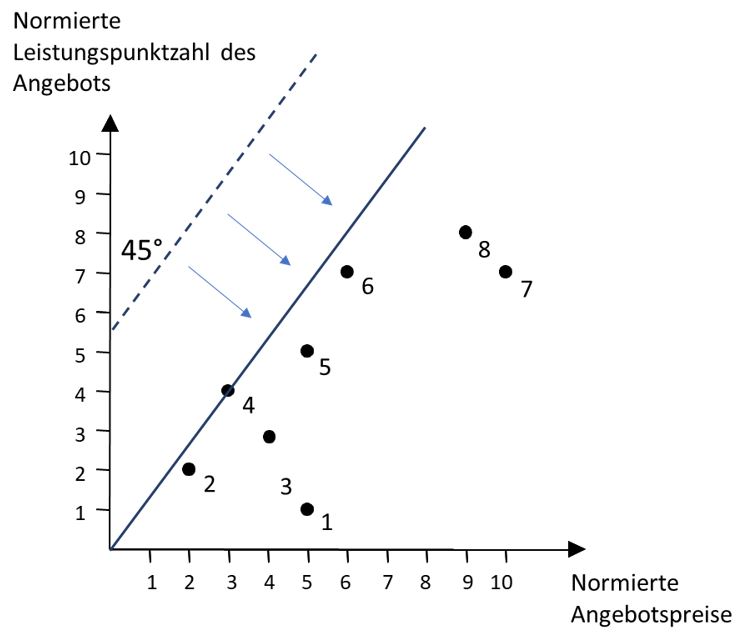
Auf der Grundlage eines solchen grafischen Vergleichs der Angebote lässt sich bereits leicht erkennen, welches Angebot relativ gesehen das beste Preis-Leistungsverhältnis hat: Dazu kann eine diagonale Linie gezogen werden, die so lange parallel nach unten geschoben wird, bis sie auf die einzelnen Angebote trifft. Das Angebot, das mit seiner Leistungs- bzw. Preisausprägung am weitesten links (günstig) und oben (leistungsstark) liegt (auf das eine diagonale Gerade also als erstes stoßen würde) ist demnach bezüglich des Preis-Leistungsverhältnisses das beste Angebot.
Ist ein Angebot mit seinen Preis- und Leistungseigenschaften auf diesem äußeren Rand der grafischen Darstellung bzw. der nach unten verschobenen Gerade verortet, nennt man es „effizient“. Kein anderes Angebot und kein Punkt auf dem dadurch definierten Rand dominiert dieses Angebot, d.h. kein Angebot ist hinsichtlich des Preises und (!) gleichzeitig hinsichtlich der Leistung mindestens genauso gut oder besser, kein Angebot besitzt relativ gesehen also ein besseres Preis-Leistungsverhältnis (und vice versa). Die oben skizzierte grafische Darstellung trifft somit die gleiche Aussage wie die Berechnung von Wertungskennzahlen mithilfe der einfachen Richtwertmethode. In obigem Beispiel hat Angebot Nr. 4. die beste Preis-Leistungs-Kennzahl bzw. die beste Bewertung gemäß der Richtwertmethode und ist „effizient“. Lägen noch andere Angebote auf der diagonalen Linie, wären diese genauso gut, würden also bei der einfachen Richtwertmethode die gleiche Wertungskennzahl erhalten bzw. wären ebenfalls „effizient“.
Die Geister die ich rief… Berücksichtigung variabler Referenzwerte bei der Wertung von Angeboten
Oftmals ist der hier nun grafisch dargestellte Zusammenhang zwischen Preis und Leistung bzw. der „effiziente Rand“ in der Praxis aber nicht linear, etwa bei innovativen Produktionsmethoden oder aufgrund von Patenten. Darüber hinaus kann die volle Erfüllung aller im Leistungsverzeichnis geforderten Leistungsaspekte einen überproportional hohen Aufwand oder überproportional ausgebaute Strukturen erfordern, wohingegen eine weniger gute Erfüllung der Leistungskriterien auch mit einem Bruchteil der Kosten realisierbar sein kann.
Ein Angebot, das mit einem Preis von 20.000 Euro und einer Leistungspunktzahl von 40 einhergeht, ist deshalb ggf. als genauso gut anzusehen, wie ein Angebot, das einen Preis von 50.000 Euro hat, dafür aber eine Leistungspunktzahl von 80, wenngleich dieses Angebot nicht „linear“ bzw. gleichmäßig besser ist, sondern mit der Erhöhung der Leistung ein überproportionaler Kostenanstieg verbunden ist, der zu einem entsprechend überproportionalen Preisanstieg führt. Denkbar ist auch, dass ein Bieter knapp aus dem Schwankungsbereich anderer Bewertungsmethoden etwa aufgrund der Leistung fiele, dafür aber einen so signifikanten Preisvorteil bietet, dass der Auftraggeber dieses Angebot doch bezuschlagen wollen würde. Lediglich die Preis-Leistungs-Verhältnisse sämtlicher Angebote statisch bzw. „linear“ miteinander zu vergleichen, wird dem Umstand, dass je nach Preis- und Leistungsniveau des betrachteten Angebots ein anderer Referenzwert bzw. eine andere Gewichtung von Preis- und Leistung angemessen wäre, also nicht gerecht.
Zeichnet man einen nichtlinearen Rand um die Alternativen, ergibt sich folgendes Bild an Angeboten, die auf einem „einhüllenden Rand“ (-> „Dateneinhüllanalyse“) mit Angeboten liegen:
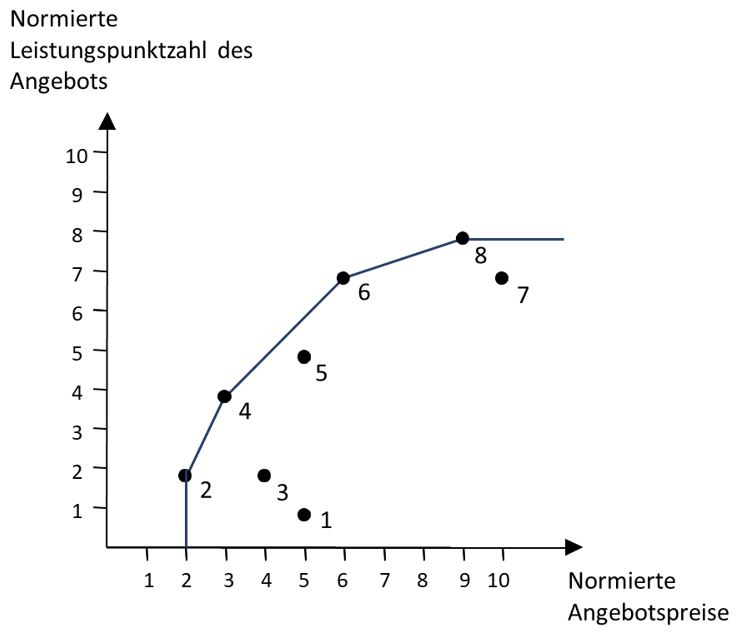
Streng genommen sind Angebot 2, 4, 6 und 8 hiernach alle gleich effizient, da der Zusammenhang zwischen Preis- und Leistung nicht linear sein muss bzw. je nach dem Niveau der Kriterienausprägungen der vorliegenden Angebote unterschiedliche Gewichtungen von Preis- und Leistungskriterien (respektive ein unterschiedliches Referenzniveau bestmöglicher Angebote) gelten.
Statt also wie bei der einfachen Richtwertmethode nur das Angebot mit dem besten Preis-Leistungsverhältnis auszuwählen oder – wie bei der erweiterten Richtwertmethode – eine bestimmte Prozentzahl von Angeboten mit den besten Preis-Leistungsverhältnissen näher zu betrachten, sollten in vielen Fällen in einer zweiphasigen Analyse aus entscheidungstheoretischer Sicht eher diejenigen Angebote weiter betrachtet werden, die einen solchen „effizienten Rand“ aufspannen, zwischen denen also entsprechend dem oftmals eigentlich nichtlinearen Verlauf des Preis-Leistungsverhältnisses keine eindeutige Entscheidung getroffen werden kann bzw. sollte. Um unter diesen verbleibenden Alternativen abschließend eine adäquate Auswahl zu treffen, müssen nicht zwangsläufig Preiskriterien (erneut) eine Rolle spielen. Denkbar sind auch eine Zuschlagserteilung nach ökologischen oder sozialen Kriterien, wenn die Angebote aus wirtschaftlicher Sicht durch die gewählte Methodik als „gleich gut“ angesehen werden können. Alternativ ist unter den verbleibenden Angeboten nach wie vor auch weiterhin die Zuschlagserteilung nach dem niedrigsten Preis möglich.
Die eigentliche Data Envelopment Analysis ist noch deutlich komplexer und widmet sich insbesondere auch der Ermittlung der Höhe der relativen Ineffizienzen abgeschlagener Alternativen. Die Analyse erfolgt zudem in der Regel auf mathematischer Basis, was insbesondere im mehrdimensionalen Fall (mit mehreren Input- (bzw. Preis) und Output- (bzw. Leistungs)faktoren) notwendig wird, da eine grafische Ausarbeitung dann nicht mehr möglich ist.[1]

Dr. Stefan Krusenbaum schult zu Wertungsmethoden regelmäßig in der cosinex Akademie. Die nächsten Seminare:
Fazit und Hinweise für die Praxis
Die in dieser Beitragsreihe vorgestellten Methoden zum Vergleich von „Äpfeln mit Birnen“ stellen einen Überblick über gängige Verfahren der mulitkriteriellen Angebotswertung dar. Während einige der aufgezeigten Verfahren relativ einfach gehalten sind, sind andere deutlich komplexer.
Die Komplexität der Methoden steigt umso mehr, je stärker versucht wird, subjektive Einflüsse durch den Anwender außen vor zu lassen. Je differenzierter also durch die Methode z.B. Gewichte oder Referenzwerte „automatisch“ ermittelt werden (wie z.B. bei den Richtwertmethoden, aber auch bei der Data Envelopment Analysis mit variablen Preis-/Leistungsreferenzwertniveaus), desto höher ist der Aufwand zur Anwendung der Methode.
Einige der vorgestellten Methoden (wie z.B. die Ermittlung aller effizienten Alternativen über die Data Envelopment Analysis und die anschließende Auswahl gemäß eines bestimmten Kriteriums) sind noch nicht im cosinex Vergabemanagementsystem berücksichtigt, können allerdings – wenn sich der Auftraggeber für die Methode entscheidet – über die Funktion „externe Wertung“ außerhalb des Systems, z.B. in Excel, durchgeführt und in der jeweiligen E-Vergabeakte dokumentiert werden. Aufgrund der (verglichen mit einer selbst vorgenommenen Vorgabe einer Preis-Leistungsgewichtung) höheren Komplexität, die sich auch in der erklärenden Beschreibung des Wertungsvorgehens in den Ausschreibungsunterlagen widerspiegeln müsste, werden solche Vorgehensweisen in der Vergabepraxis momentan aber kaum angewandt.
Um sich solchen komplexeren Methoden in der Vergabepraxis zu nähern, lohnt es, sich zunächst die Grundideen bzw. Vorteile dieser Methoden zu verdeutlichen und verschiedene Methoden exemplarisch auf bereits abgeschlossene Ausschreibungen anzuwenden. So kann sich eine Vergabestelle durch die grafische Gegenüberstellung von Preis- und Leistungsausprägungen der verschiedenen Angebote z.B. leicht vergegenwärtigen, ob sich in der Vergangenheit unter Angeboten, die im Rahmen eines bestimmten Wertungsverfahrens ausgeschlossen wurden, nicht ggf. sogar „effiziente Angebote“ befanden. Hierrüber kann recht einfach und risikofrei das Veränderungs- und ggf. Verbesserungspotential alternativer Wertungsmethoden nachvollzogen werden.
Alle Teile der Reihe
- Teil 1 befasst sich neben einer Einführung mit der Wertungsmethode niedrigster Preis.
- Teil 2 gibt einen Überblick über die Methoden der Wertungsklasse Preis-Kriterien-Gewichtungen.
- Teil 3 analysiert die Wertungsklasse der Richtwert-Methoden.
- Teil 4 stellt weitere, im Bereich des öffentlichen Auftragswesens noch nicht gängige, Wertungsmethoden vor.
[1] Spätestens in einer mehrdimensionalen Analyse müsste durch ein Optimierungsverfahren berechnet werden, ob sich für ein Angebot eine derartige Gewichtung der Preis- und Leistungskriterien („Aufspannung eines umhüllenden effizienten Randes“) finden lässt, dass ebendiese Gewichtung (bzw. Linearkombination) auf die Preis- und Leistungskriterien anderer Angebote angewandt nicht zu einer besseren Bewertung dieser übrigen Angebote führt.
Verwandte Beiträge
Bildquelle: DDRockstar – fotolia.de

